Todo empezó con Demócrito y Leucipo, constituyeron que la materia podría estar formada por «A-tomos» (Partículas no indivisibles) y que entre ellos habría vacío.
Aristóteles estableció la teoría de los 4 elementos, en la cual la materia era combinación de aire, fuego, agua o tierra.
Los alquimistas siguieron la teoría aristotélica para intentar obtener la piedra filosofal es decir una forma de transmutar metales en oro, curar enfermedades y evitar la muerte o incluso envejecer.
La teoría de Demócrito y Leucipo cayeron al olvido hasta que en 1808 John Dalton la recupera, estableciendo que los á-tomos se unen para formar compuestos.
1887 con la llegada de la electricidad se descubre el electrón a partir de los tubos de rayos catódicos por parte de J.J Thomson.
Este se puede afirmar que es el 1º modelo de átomo compuesto:
Los electrones, pequeñas partículas con carga eléctrica negativa, estarían incrustadas en una nube de carga positiva de forma similar a las pasas en un pastel.
En 1911 E. Rutherford prueba si la teoría de J.J. Thomson es correcta o no, a partir del siguiente experimento:
Rutherford usa partículas alfas, procedentes de un material reactivo, que se les hace acelerar e incidir sobre una lámina de oro muy delgada
Tras atravesar la lámina las partículas α chocan contra una pantalla recubierta interiormente de sulfuro de zinc, produciéndose un chispazo. De esta forma era posible observar si las partículas sufrían alguna desviación al atravesar la lámina.
- La mayor parte de las partículas atravesaban la lámina de oro sin sufrir ninguna desviación.
- Muy pocas (una de cada 10.000 aproximadamente) se desviaba un ángulo mayor de 10 grados (trazo a rayas)
- En rarísimas ocasiones las partículas α rebotaban (líneas de puntos)
Si el modelo atómico propuesto por Thomson fuera cierto no deberían observarse desviaciones ni rebotes de las partículas incidentes. Éstas atravesarían limpiamente los átomos sin desviarse.
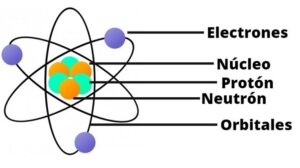
Modelo planetario de átomo propuesto por Rutherford en 1911
- Para que las partículas se desvíen deben encontrar en su trayectoria una zona llamada núcleo en la que se concentre carga de signo positivo y cuya masa sea comparable o mayor a la de las partículas α (alfas).
- La zona en la que se concentra la masa y la carga positiva debería de ser muy pequeña comparada con la totalidad del átomo.
- Los electrones orbitan en círculos alrededor del núcleo.
Inconvenientes de la Teoría propuesta por Rutherford
Contradecía la teoría electromagnética de Maxwell:
El hecho de que las ondas electromagnéticas se propagaran con idéntica
velocidad que la luz llevó a la consideración de que la luz misma no es más que una onda electromagnética. La teoría de Maxwell unificaba así óptica y electromagnetismo.
Según esta teoría una carga eléctrica acelerada debería de emitir ondas electromagnéticas.
Por ese motivo un electrón en círculos alrededor del núcleo debería emitir ondas electromagnéticas. Dicha emisión provocaría una perdida de energía que haría que el electrón describiera órbitas de radio decreciente hasta caer al núcleo.
No daba explicación a los espectros atómicos
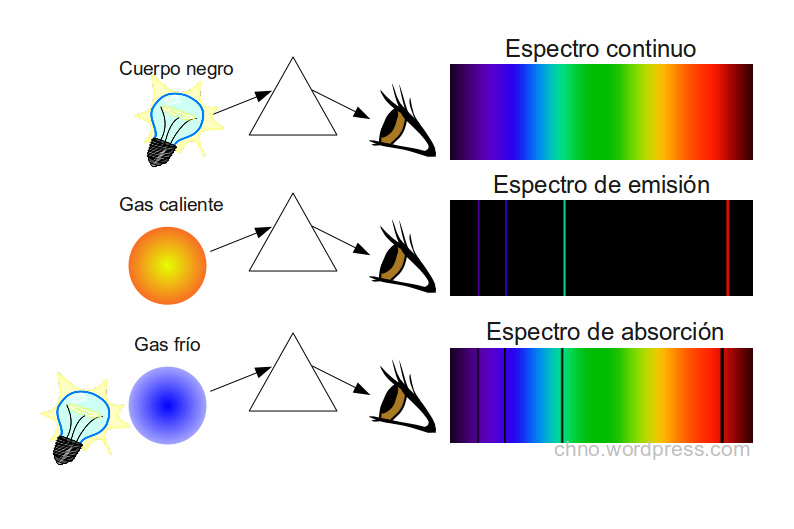
Si encerramos en un tubo hidrógeno o helio y sometemos el gas a voltajes elevados, el gas emite luz. Si hacemos pasar esa luz a través de un prisma, los colores que la constituyen se separan dándonos el espectro de la luz analizada.
Pronto se concluyó que la emisión de luz podría deberse a que los electrones absorbían energía de la corriente eléctrica y saltaban a órbitas superiores para, a continuación, volver a caer a las órbitas más próximas al núcleo emitiendo el exceso de energía en forma de energía luminosa.
Esta interpretación conducía, sin embargo, a afirmar que los espectros deberían de ser continuos, ya que al existir órbitas de cualquier radio (y energía) todos los saltos son posibles. La experiencia, por el contrario, mostraba que los espectros de los átomos son discontinuos. Constan de rayas de diversos colores sobre
un fondo negro
En 1918 Rutherford propuso el nombre de la partícula fundamental protón perteneciente a los núcleos de hidrógeno gracias a la reacciones nucleares.
El neutrón también fue propuesto por Rutherford en 1920, finalmente acabo siendo identificado por Rutherford en 1932 como producto de la reacción nuclear producida al bombardear núcleos de berilio con partículas alfa.
El diámetro de un átomo típico es del orden de 10-10 m (0,1 nm), mientras que el núcleo atómico es 10 000 veces más pequeño (10-14 m).
Los protones y neutrones tienen un diámetro del orden de 10 -15 m, y el diámetro del electrón es del orden de 10 -18 m.
Física Cuántica. Modelo atómico de Bohr
Niehls Bohr propone en 1913 un nuevo modelo atómico apoyado en tres postulados:
- Cualquiera que sea la órbita descrita por un electrón, este no emite energía.
Las órbitas son consideradas como estados estacionarios de energía.
A cada una de ellas le corresponde una energía, tanto mayor, cuanto más alejada se encuentre del núcleo. - No todas las órbitas son posibles. Únicamente pueden existir aquellas órbitas para las cuales el momento angular del e– sea un múltiplo entero de h/(2π) = h (léase «hache cruzada»)
m*v*r=n*(h/2π)
El número, n, que determina las órbitas posibles, se denomina número cuántico principal.
Las órbitas que se correspondan con valores no enteros del número cuántico principal, no existen. - La energía liberada al caer un e– desde una órbita superior, de energía E2, a otra inferior, de energía E1 , se emite en forma en cuanto de luz (fotón).
La frecuencia (f) del cuanto viene dada por la expresión:
E2 – E1 =h*f
h(contante de Planck) = 6,62*10-34
Excelentes resultados, pero contradicen estas leyes:
- 1º Postulado va en contra de la teoría electromagnética de Maxwell
- 2º Postulado En la física clásica era inaceptable suponer que el electrón no pudiera orbitar a determinadas distancias del núcleo, o que no pudiera tener determinados valores de energía
- La afirmación era equivalente a suponer que un objeto que describe circunferencias atado a una cuerda, no puede describir aquellas cuyo radio no seamúltiplo de dos (por ejemplo).
- 3º Postulado afirmaba que la luz se emitía en forma de pequeños paquetes o cuantos
- lo cual a pesar de que ya había sido propuesto por Planck en 1900, no dejaba de sorprender en una época en la que la idea de que la luz era una onda estaba firmemente arraigada
Ampliación
Estudiando la distribución de líneas del espectro visible del hidrógeno Balmer en 1885 había deducido que la posición de las líneas respondía a la siguiente fórmula matemática:

La ley de Coulomb nos permite calcular la fuerza con la que un electrón (de carga e) es atraído por el núcleo de carga Ze (el número de protones, o cargas positivas del núcleo, viene dado por el número atómico, Z):
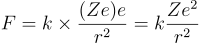
(Z=1 para el átomo de H)
Imponiendo la condición para que el electrón describa una circunferencia obtenemos:
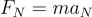

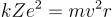
Teniendo en cuenta el segundo postulado de Bohr, tenemos:
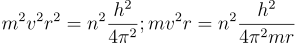
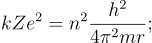
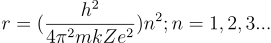
Esta expresión permite calcular el radio de las órbitas permitidas. Como se puede observar existe una condición de cuantización, impuesta por los valores permitidos de n (número cuántico). De esta manera son posibles las órbitas para las cuales n tenga valores enteros, mientras que no existen aquellas órbitas para las cuales n no sea entero.
La frecuencia de las líneas que aparecen en el espectro puede ser calculada ahora si tenemos en cuenta la cuantización de las órbitas:
La energía de un electrón que orbita alrededor de un núcleo, con carga Ze, viene dada por:

Introduciendo el valor del radio obtenido para las órbitas posibles obtenemos:
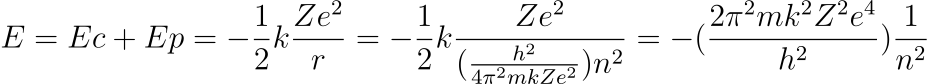
Sustituyendo el valor obtenido para la energía en la expresión que da la frecuencia de la luz emitida(tercer postulado) tenemos:
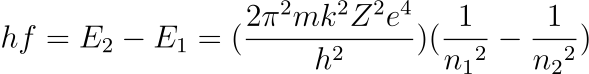
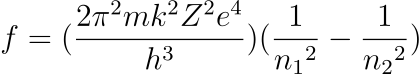
Considerando que n1 = 2 para el espectro visible del átomo de hidrógeno (lo que equivale a decir que la luz visible del espectro del hidrógeno se emite cuando los electrones caen desde órbitas superiores a la segunda orbita), tenemos que las frecuencias deberían responder a la expresión;
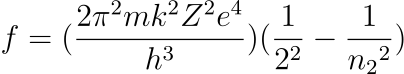
La expresión obtenida concuerda con la obtenida experimentalmente por Balmer.
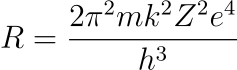

En espectroscopía se utiliza una fórmula similar conocida como fórmula de Rydberg.
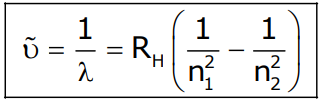
La constante RH para el átomo de hidrógeno, llamada constante de Rydberg, vale: 1,0967757 107 m-1
Con esta fórmula se pueden calcular las distintas líneas para el espectro del átomo de hidrógeno que se pueden clasificar en distintas series.
Serie de Lyman. Constituida por las líneas que aparecen cuando los electrones caen desde órbitas superiores a la primera órbita (n1 = 1; n2 =2,3,4…). Las líneas de esta serie se sitúan en el ultravioleta.
Serie de Balmer. Formada por el conjunto de líneas obtenidas cuando los electrones caen desde órbitas superiores a la segunda órbita (n1 = 2; n2 =3,4,5…). Las líneas de esta serie se sitúan en el visible.
Serie de Paschen. Integrada por el conjunto de líneas obtenidas cuando los electrones caen desde órbitas superiores a la tercera órbita (n1 = 3; n2 =4,5,6…). Las líneas de esta serie se sitúan en el infrarrojo.
También existen las series de Brackett y Pfund, situadas también en el infrarrojo y formadas por el conjunto de líneas que se obtienen al caer a la cuarta orbita (n1 = 4) y a la quinta órbita (n1 = 5), respectivamente.
Se calculan a continuación las longitudes de las líneas correspondientes a la serie de Balmer para el hidrógeno.

Valores medidos experimentalmente
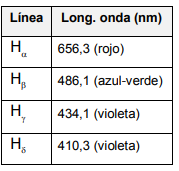

Se puede observar que la concordancia con las medidas experimentales es muy buena
Extensión de Sommerfeld. Órbitas elípticas
En 1916 Sommerfed perfeccionó el átomo de Bohr considerando que si el electrón está sometido a una fuerza inversamente proporcional al cuadrado de la distancia (ley de Coulomb), debería de describir una elipse no una circunferencia.
Según la teoría desarrollada por Bohr un electrón no puede poseer valores arbitrarios de energía cuando orbita alrededor del núcleo, hay valores permitidos y valores prohibidos, ya que existen órbitas permitidas y otras que están prohibidas. La energía está «cuantizada».
Para fijar una elipse necesitamos determinar fijar dos parámetros: el valor del semieje mayor y del semieje menor.
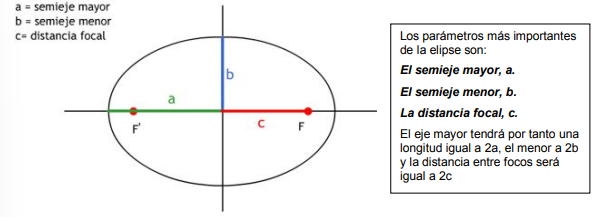
Para determinar las posible órbitas elípticas necesitamos dos números cuánticos:
n: Número cuántico principal. Cuantiza (fija) el semieje mayor.
l: Número cuántico secundario. Cuantiza (fija) el semieje menor.

Quiere decir que existe :
Para un valor fijo de n (un nivel de energía dado), pueden existir varios orbitales con diferentes formas (más alargados o más redondeados), dependiendo del valor de l.
Es decir, la energía puede ser la misma (misma n), pero la forma del orbital puede variar (según l).
El número cuántico secundario solamente puede tomar los valores enteros comprendidos entre 0 y n-1:
I=0,1,2,3… (n-1)
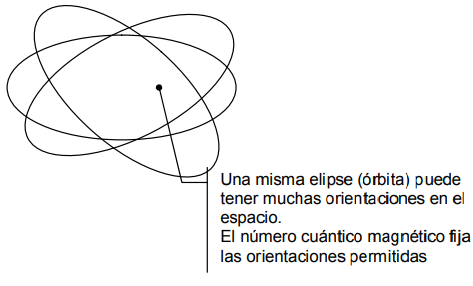
Si consideramos un espacio tridimensional, vemos que las elipses (órbitas electrónicas) pueden adquirir diversas orientaciones.
Otro número cuántico, ml , número cuántico magnético, fija (cuantiza) las orientaciones permitidas.
El número cuántico magnético adquiere valores enteros comprendidos entre -l y +l ( incluyendo el valor cero).
ml =-l…0…+l
Las órbitas posibles, en consecuencia, quedan fijadas por tres números cuánticos:
- n : Número cuántico principal.
- Cuantiza (fija) el semieje mayor de la órbita (elipse).
- Valores: n =1, 2, 3 …
- l : Número cuántico secundario.
- Cuantiza (fija) el radio menor de la órbita (elipse).
- Valores: l =0, 1, 2, 3 … (n-1)..
- ml : Número cuántico magnético.
- Cuantiza (fija) la orientación de la órbita en el espacio.
- Valores: ml = – l … 0 … +l
A cada órbita, determinada por los tres números cuánticos, le corresponde un valor de energía.
Si ahora consideramos al electrón como una partícula situada en determinada órbita, a la energía de la órbita hemos de sumar una energía propia del electrón (podemos imaginar el electrón como una partícula que gira sobre su propio eje). Esta energía está también cuantizada (es decir, no puede tomar cualquier valor) y es función de un cuarto número cuántico, ms, llamado «número cuántico de spin».
En resumen, la energía de un electrón situado en una órbita es función de cuatro números
cuánticos: tres que fijan el valor de la energía de la órbita considerada: n, l y ml, y el número cuántico de spin, ms, que cuantiza la energía propia del electrón:
EElectrón = f (n, l, ml, ms)
Una vez que conocemos los distintos niveles de energía en los que pueden situarse los electrones el siguiente paso será calcular su energía y ordenarlos según un orden creciente. Cuando se trata de hacer eso se comprueba que en condiciones normales (ausencia de campos magnéticos) los valores de energía dependen únicamente de los valores de los números cuánticos n y l. Es decir, aquellos estados de energía que difieren en el valor de ml tienen la misma energía (se dice que son degenerados).
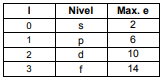
Por razones históricas los niveles con l =0 se nombran como «s»; «p» cuando l=1; «d» si l=2, y «f» para l=3.

Para recordar el orden de energía (de menor a mayor) se recurre al llamado diagrama de Möeller:
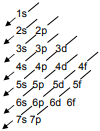
Se puede observar que a partir de la tercera capa estados con un valor de n superior (por ejemplo el 4s) pueden tener menos energía que otros con un valor de n inferior (por ejemplo el 3d).
En general, cuanto mayor es n+l, mayor es la energía
A la hora de ir llenando con electrones los distintos estados de energía disponibles hay que tener en cuenta el llamado Principio de Exclusión de Pauli:
No pueden existir dos electrones con los cuatro números cuánticos iguales
Podemos determinar el número máximo de electrones que pueden situarse en un nivel energético dado aplicando el principio de Exclusión de Pauli:
Para n = 1 (primera órbita), l sólo puede tomar un valor: l = 1 – 1 = 0. En consecuencia ml = 0 y s = +1/2 y -1/2. Luego para la primera órbita existen dos posibles valores de energía para el electrón:
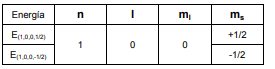
Para n =2 (segunda órbita), l puede tomar valores desde cero hasta l = 2-1 =1. Por tanto: l =0, 1.
- Para l =0, y según lo visto más arriba, existen dos posibles valores de energía:
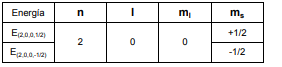
- Para l =1, ml puede tomar tres valores: -1, 0, 1, y teniendo en cuenta los dos valores posibles para el número cuántico de spin, tendremos un total de seis estados de energía distintos:

Para n =3 (tercera órbita), l puede tomar valores desde cero hasta l = 3-1= 2. Por tanto, tres valores: l =0, 1 y 2
- Para l =0 y l = 1 ya se ha visto que son posibles dos y seis estados de energía. Para l = 2, ml puede tomar cinco valores: -2, – 1, 0, +1, +2, y teniendo en cuenta los dos valores posibles para el número cuántico de spin, tendremos un total de diez estados de energía distintos.
Para n =4 (cuarta órbita), l puede tomar valores desde cero hasta l = 4-1= 3. Cuatro valores: l = 0, 1, 2 y 3
- Para l = 3 ml puede tomar siete valores: -3, -2, – 1, 0, +1, +2, +3, y teniendo en cuenta los dos valores posibles para el número cuántico de spin, tendremos un total de catorce estados de energía distintos.
Se concluye que en un estado “s” puede haber como máximo dos electrones, seis en uno “p”, diez en un “d” y catorce en un “f”
Configuración electrónica de los átomos
Con todos estos datos la configuración electrónica de un átomo (esto es, la distribución de sus electrones entre los estados de energía posibles) se obtiene siguiendo las siguientes normas:
Para obtener la configuración electrónica de un átomo:
- Considerar el número de electrones que se deben distribuir. Recordar que el número de electrones en un átomo neutro viene dado por el número atómico Z.
- Los electrones se van distribuyendo entre los estados de energía posibles llenando primero los de menor energía. Cuando un nivel se complete, pasar al siguiente (recordar el principio de exclusión y para establecer el orden de llenado usar el diagrama de Möeller).
- La configuración final debe darse ordenada por capas.
Si queremos afinar un poco más en la configuración electrónica deberemos usar el Principio de Máxima Multiplicidad o Regla de Hund que establece que a la hora de ocupar estados de energía degenerados (por ejemplo los tres estados»p») los electrones tienden a situarse en ellos con idéntico spin.
Apliquemos esto para el átomo de nitrógeno (Z=7). Representaremos los estados posibles por cuadrados y el valor del spín por una flecha que apunta hacia arriba cuando el spin valga +1/2 y hacia abajo cuando valga -1/2
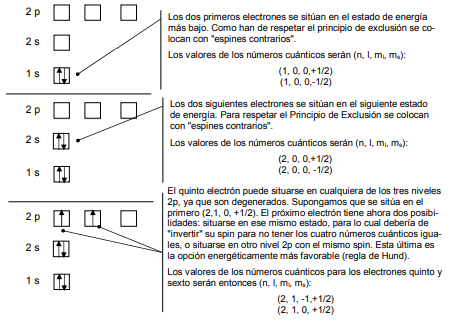

Sabemos que la configuración ns2p6(configuración de gas noble) en la última capa es especialmente estable.
Aunque la estabilidad es considerablemente menor que la correspondiente a la estructura de gas noble, también presentan una estabilidad considerable las estructuras que se corresponden con los niveles p o d llenos o semillenos. Para alcanzarlas algunos elementos pueden promocionar electrones desde niveles
de energía inferior a niveles superiores. Este efecto se observa, sobre todo, entre los metales de transición, en los cuales los niveles (n-1) d y ns están muy próximos energéticamente.
Este efecto es muy importante en la química del carbono el cual, a pesar de tener como estructura teórica 1s2 2s2 p2, presenta la configuración 1s2 2s1 p3 en la mayoría de sus combinaciones. La energía empleada en promocionar un electrón de un nivel 2s al 2p se compensa con creces al formar cuatro enlaces covalentes en vez de dos.